Play CartPole game with Nature-DQN
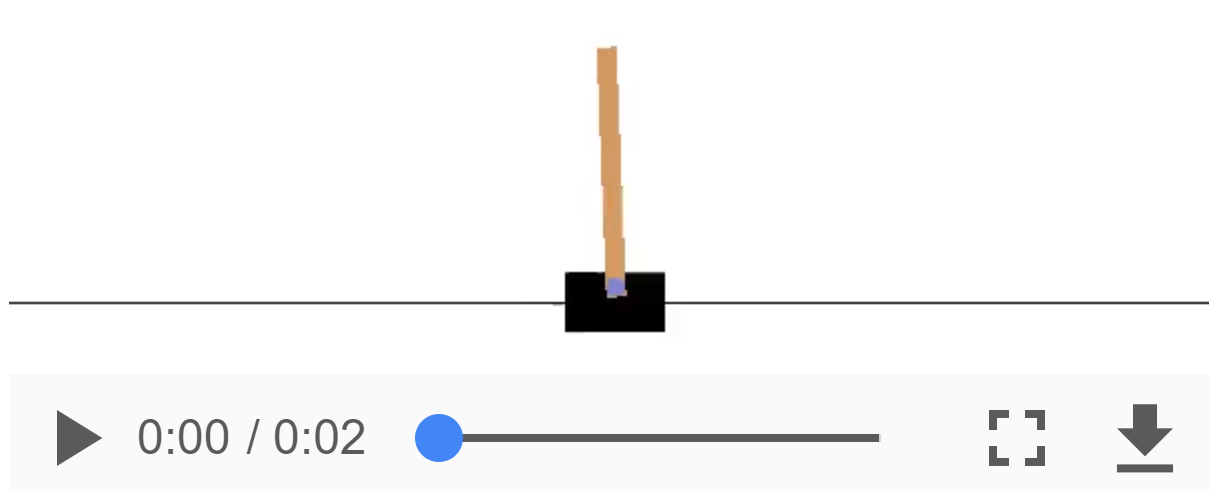
Recently, people are focusing on the playing of games by computers. There are so many people curious about that why computer score so high and even higher than human. In this blog, we will try to make a smart computer to play CarPole game.
The method adopted by this blog is Nature Deep Q Network(Nature DQN)[1]. We will play CartPole game created by OpenAI[2]. It’s a very easy game, the player need move the box to left or right to make the stick stand. Normally, the simulation will end before the cart-pole is allowed to go off-screen.
1 Introducing of Our Nature-DQN in CartPole Game
Before the introducing of our DQN, we need familier with the game environment. In CartPole game, the size of action space is 2, it means that all what we can do are moving the black box left or right. And at the same, we will score 1 in each step if our stick still stand after our operation.
In our DQN, the reward function is defined as flow:
In which the is the immediately reward got back from the CartPole game, and the value of it is a constant 1.
We use normal Q-learning algorithm and MSE loss:
In which the is our state-action function, and the is learning rate. In detail, our loss function also can be defined as:
In this blog, we will adopt the experience replay and target network to make the performance of our method better. We will explain them in our code. if you want our full code, click here
2 Our method
2.1 Dataset
About our dataset, we adopt the experience relay strategy. In experience relay, we store past several action and reward histories. We sample from the stored action-reward paires to train our network.
Our dataset manager looks like:
class datasetutil():
...
def add_action(self, origin_state, action, reward, next_state):
if len(self.dataset_buff) >= self.config['buff_size']:
del self.dataset_buff[0]
self.dataset_buff.append([origin_state, action, reward, next_state])
...
def sample(self, batch_size=32):
sample_idx = np.random.choice(len(self.dataset_buff),
size=batch_size)
origin_state = np.array([self.dataset_buff[i][0] for i in sample_idx])
action = np.array([[self.dataset_buff[i][1]] for i in sample_idx])
reward = np.array([[self.dataset_buff[i][2]] for i in sample_idx])
next_state = np.array([self.dataset_buff[i][3] for i in sample_idx])
return origin_state, action, reward, next_state
2.2 Network
In fact we establish two networks: eval_network and target_network. They has same structure. The only difference between them is that the parameters of target_network lags behind several epoch. We will explain the training detail in next section.
The architecture of our network is so simple. It consist of three linear layer. In our experiments, we also try the architecture which only consist of two linear layer and get the similar result.
We will show the core code here:
class net(nn.Module):
def __init__(self, **args):
super(net, self).__init__()
self.linear1 = nn.Linear(args['n_states'], args['n_hidden'])
# self.linear2 = nn.Linear(args['n_hidden'], args['n_actions'])
self.linear2 = nn.Linear(args['n_hidden'], args['n_hidden'])
self.linear3 = nn.Linear(args['n_hidden'], args['n_actions'])
def forward(self, x):
x = F.relu(self.linear1(x))
x = F.relu(self.linear2(x))
x = self.linear3(x)
return x
class qlearning():
def __init__(self, **args):
...
self.eval_net = net(n_states=self.config['n_states'],
n_hidden=self.config['n_hidden'],
n_actions=self.config['n_actions'])
self.target_net = net(n_states=self.config['n_states'],
n_hidden=self.config['n_hidden'],
n_actions=self.config['n_actions'])
self.target_net.train(False)
...
2.3 Learning with DQN
In CartPole game, we will get 1 reward after every successful action. So our immediately reward can not just define as 1. In our experiments, we define our reward function as:
As increasing, the value of close to:
What’s more, in the process of training, we use algorithm to generate the next action. The detail shows bellow:
def select_action(self, state, epsilon_greedy=True):
self.eval_net.train(False)
if epsilon_greedy is False or \
np.random.uniform() < self.config['epsilon']:
state = Variable(torch.Tensor(state))
action_score = self.eval_net(state).squeeze().data.numpy()
action = np.argmax(action_score)
else:
action = np.random.randint(0, self.config['n_actions'])
return action
We train our network with MSE function, and Adam optimizer. The detail of our training strategy shows bellow:
class qlearning():
...
def train(self, origin_state, action, reward, next_state):
# Nature DQN
self.eval_net.train(True)
self.optimizer.zero_grad()
eval_score = self.eval_net(Variable(torch.Tensor(origin_state)))
next_score = self.target_net(Variable(
torch.Tensor(next_state))).data.numpy()
target_score = copy.deepcopy(eval_score.data.numpy())
for i in range(len(target_score)):
target_score[i][action[i][0]] = reward[i][0] + \
self.config['gamma'] * np.max(next_score[i])
target_score = Variable(torch.Tensor(target_score))
loss = self.loss_func(eval_score, target_score)
loss.backward()
self.optimizer.step()
return float(loss.mean().data.numpy())
def copy_parameters(self):
eval_state_dict = self.eval_net.state_dict()
target_state_dict = self.target_net.state_dict()
for name, param in eval_state_dict.items():
target_state_dict[name].copy_(param)
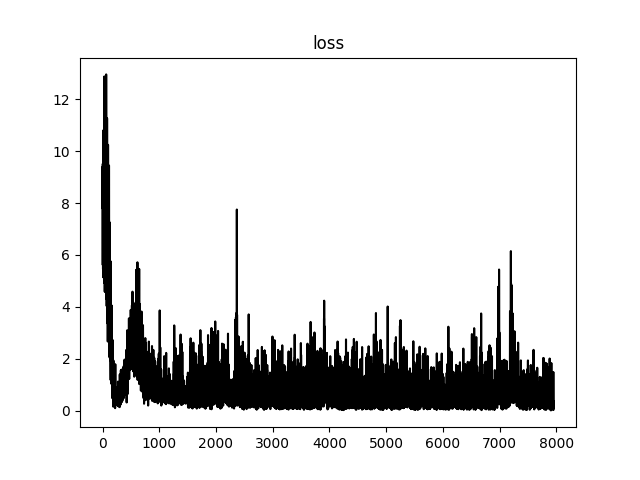
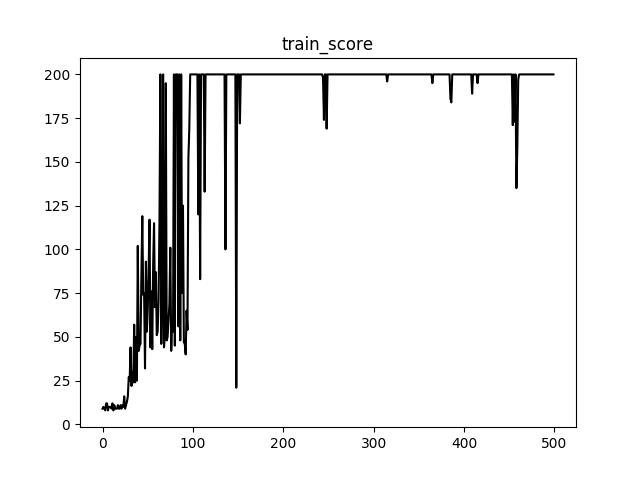
3 Result
Loss
Score in process of training
Score in process of testing

4 Reference
1. Playing Atari with Deep Reinforcement Learning
2. http://gym.openai.com/